Reactivity in Chemistry
Reaction Kinetics
RK4. Rate Constants
There is a measurable parameter that can be used to get an idea about the activation barrier of a reaction. It is called the rate constant. The rate constant for a reaction is related to how quickly the reaction proceeds. A large rate constant corresponds to a very fast reaction. A very small rate constant corresponds to a slow one.
The rate constant is an index of the speed of the reaction.
Rate constants have different units depending on how the reaction proceeds, but just to give you a feel for how they vary, a reaction with a "first order" rate constant of 0.001 s-1 (or 10-3 s-1; you'll learn what "first order" means later) would be over in about an hour. A reaction with a first order rate constant of 10-6 s-1 might take a couple of weeks.
The rate constant gives direct insight into what is happening at the transition state, because it is based on the energy difference between the reactants and the transition state. Based on that information, we get some ideas of what is happening on the way to the transition state.
The rate constant can be broken down into pieces. Mathematically, it is often expressed as
k = (RT/Nh) e -Δ G/RT
In which R = the ideal gas constant, T = temperature, N = Avogadro's number, h = Planck's constant and D G = the free energy of activation.
The ideal gas constant, Planck's constant and Avogadro's number are all typical constants used in modeling the behaviour of molecules or large groups of molecules. The free energy of activation is essentially the energy requirement to get a molecule (or a mole of them) to undergo the reaction.
Problem RK4.1.
For each of the following pairs, use < or > to indicate which quantity is larger.
a) e 2 or e 10
b) e 1/4 or e 1/2
c) e -3 or e -4
d) e -1/2 or e -1/3
Note that k really depends on just two variables:
The ratio of activation free energy to temperature compares the energy needed to the energy available. The more energy available compared to the energy needed, the lower this ratio becomes. As a result, the exponential part of the function becomes larger (since the power has a minus sign). That makes the rate constant bigger, and the reaction becomes faster.
Large groups of molecules behave like populations of anything else. They have averages, as well as outliers on the high and low end. However, the higher the temperature, the more energy a group of molecules will have on average.
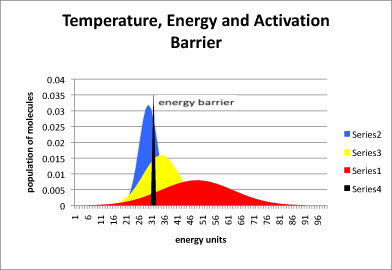
In the following drawing, the blue curve represents the energy content in a population of molecules at low temperature. The peak of the curve is near the average energy for this collection of molecules. Some of the molecules have more energy than average (they are further to the right on the blue curve) and some have less (further to the left).
The black slice through this curve indicates how much energy is needed to get over the activation barrier for a particular reaction. Notice that, at low temperature, not that many molecules have enough energy to get over the barrier at any one time. The reaction will proceed very slowly. Nevertheless, more energy is probably available from the surroundings, and so after some time most of the molecules will have obtained enough energy so that they can eventually hop over the barrier.

Figure RK4.1. The relationship between temperature and the average energy of molecules in a system.
The yellow curve represents molecules at a higher temperature, and the red curve is a population at a higher temperature still. As the temperature is increased, larger and larger fractions of the molecules have enough energy to get over the activation barrier, and so the reaction proceeds more quickly.
the rate constant compares energy needed to energy available
based on that comparison, a specific fraction of the population will be able to react at a time
This site was written by Chris P. Schaller, Ph.D., College of Saint Benedict / Saint John's University (retired) with other authors as noted on individual pages. It is freely available for educational use.

Structure & Reactivity in Organic,
Biological and Inorganic Chemistry by
Chris Schaller
is licensed under a
Creative Commons Attribution-NonCommercial 3.0 Unported License.
Send corrections to cschaller@csbsju.edu
This material is based upon work supported by the National Science Foundation under Grant No. 1043566.
Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
Navigation:
Back to Web Materials on Structure & Reactivity in Chemistry