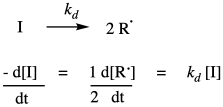
Kinetics and Thermodynamics in Polymer Chemistry
KP3. Kinetics of Chain Polymerization
The polymerization of alkenes occurs in a very different way than monomers that undergo condensation reactions. Whether it occurs through an anionic, cationic, or radical mechanism, polymerization of alkenes involves a chain reaction. Chain reactions are classically illustrated by radical chemistry, so we will look at a treatment of radical chain polymerization to see some of the factors that influence polymerization rates.
A typical radical polymerization starts with the thermal decomposition of a radical initiator to provide two radicals. The rate of decomposition depends only on the decomposition rate constant and the concentration of the initiator.
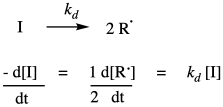
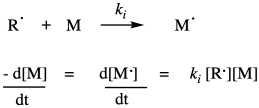
Once the radicals have been generated, they are able to undergo radical addition to a monomer double bond. Of course, radical addition to a double bond results in a new radical where the double bond used to be. Although this is formally a radical propagation step, in polymer chemistry it is termed the initiation step, because it is the first time a monomer has undergone radical addition. This step consumes the first monomer and produces a new radical species which will become the growing radical chain. It requires a collision between the radical and a monomer, so the rate of initiation depends on those two concentrations and the chain initiation rate constant, ki.
That rate law depends on a reactive intermediate. It's not a very helpful rate law, because the reactive intermediate isn't something that we have directly measured out and added to the reaction, and it might not even occur at high enough levels that we can measure its concentration as the reaction progresses. We usually look for ways to express the rate law in ways that do not include reactive intermediates. In this particular situation, the way of getting around this situation is to assume that the decomposition of the initiator is the rate determining step. Making the radicals in the first place is probably the slow part because it is heavily dependent on bond breaking, which is energy intensive. Once we have radical, it probably undergoes addition to a monomer fairly quickly, initiating chain growth. If that's true, we can assume that the chain initiation step proceeds very quickly afterward, so that the rate really depends only on the rate of the decomposition step.
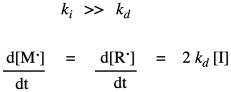
In practice, polymer chemists add another factor to the rate law. This factor, f, takes into account the fact that only some of the radicals from the initiator actually react with monomers to initiate growing chains. The rest decay through some other side reactions. Usually, f is assumed to be around 0.5.
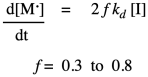
Once the first monomer has been initiated into a radical, it can react with another monomer to enchain it and make a new radical. This is the principal propagation step of the chain reaction. That step will keep repeating, adding more monomers into the chain. The rate constant for this step, kprop or kp, is identical no matter how many monomers have been enchained, but is distinct from ki because of the different nature of the radical intermediates in the two different steps. For example, the radical obtained from addition to styrene looks pretty similar whether it is the first in the chain or the tenth. Each time, the rate of consumption of monomer depends on the propagation rate constant, the concentration of the monomer, and the concentration of the propagating radical. Notice that in the rate law we just write that propagating radical the same way (M dot) no matter how long the chain grows.
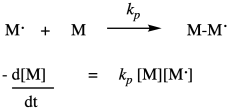
There is one last process, or group of processes, to complete the chain reaction cycle. In termination, two radicals combine in some way to form closed-shell products. There are a variety of ways that can happen in a radical polymerization. The simplest event conceptually is coupling, in which two radical chains come together and form a bond. That idea is shown below.
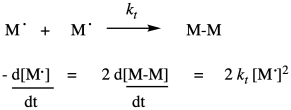
Of course, that rate depends on the termination rate constant and the concentrations of both growing chains. The same would be true if the reaction terminated by conproportionation, in which one radical abstracted an alpha hydrogen from the other, forming one saturated and one unsaturated product.
Once again, these last two rates -- of propagation and of termination -- depend on concentrations of reactive intermediates, which we do not typically know. This time we will use a very standard assumption, which is that the concentration of this reactive species remains constant, being consumed as soon as it is generated. The usual way that we apply the steady state approximation is to assume zero change in concentration of the reactive intermediate. That means that the sum of all the rates for processes generating the intermediate equal the sum of all the rates consuming the intermediate. In polymer chemistry, we take a slight shortcut, and just assume that the rate of appearance of the radical in the first place equals its rate of disappearance. We already have expressions for both of those rates.

By rearranging, we can get an expression for the reactive chain end concentration. Then we can just substitute the result into our expression for propagation rate:
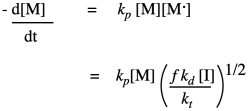
The result sums up the factors that control the growth rate for the polymer. The growth rate increases linearly with the concentration of monomer, and as the square root of the initiator concentration. The rest of the factors are just constants, so we can think of the rate law as one combined constant and those two concentration dependences. Sometimes an aggregate constant of this type is just designated k'.
Note that the propagation rate varies linearly with the concentration of growing chains, but that the termination rate varies with square of the concentration of growing chains. That difference is significant, and it underlies the strategy of living polymerization, which is to keep the concentration of growing chains low. Doing so has the adverse affect of slowing the rate of propagation, but the effect on the termination rate is much greater, making this trade-off worth it to achieve enhanced molecular weight control.
Problem KP3.1.
Suppose the following data were obtained for a radical polymerization conducted at various starting concentrations of monomer. If all of the data were conducted at an initiator concentration of 0.25 mmol L-1, calculate k'.
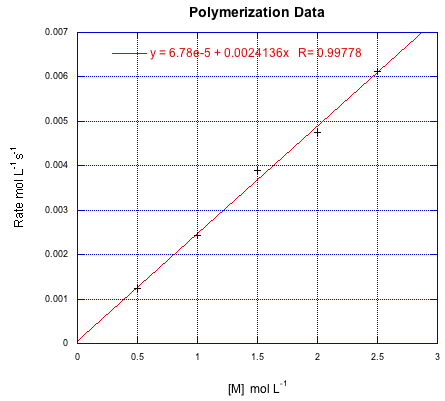
Kinetics can also be used to establish a theoretical polymer chain length. This quantity is called kinetic chain length, represented by "vee bar". In principle, it's just the ratio of the chain propagation rate to the chain initiation rate. That should tell us the number of monomers per each chain initiated. Because of our earlier assumption about the initiation rate equalling the termination rate, we can subsitute the terms for those two rates and simplify the result.

Substituting our earlier expression for the concentration of the growing radical chain ends gives a new expression.
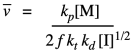
That means that we can theoretically control the length of polymer chains, because the average length should vary linearly with the concentration of monomer and inversely with the square root of initiator concentration.
As chain reactions, cationic and anionic polymerizations have some characteristics in common with radical polymerizations. One key difference is that the initiator does not fragment into two pieces, each capable of initiating a chain; instead, one added initiator starts polymerization of one chain, without the prior decompositions step seen in radical reactions. Also, termination steps in radical reactions are dominated by radical recombinations (as well as other variations), but in anionic and cationic terminations it is more likely that the growing chain encounters an impurity and reacts with that.
Problem KP3.2.
Given that for a cationic polymerization:
Rateinit = ki [M][I] and Rateterm = kt[M+]
Provide a steady state expression for the concentration of growing cationic chain.
Problem KP3.3.
If the propagation step in a cationic polymerization is written as follows:
M+ + M → M-M+
Provide the rate expression for cationic polymerization.
Problem KP3.4.
By analogy to radical polymerization, the kinetic chain length in cationic polymerization can be expressed as the ratio of propagation rate to initiation rate. Provide an expression in terms of constants and known concentrations.
Problem KP3.5.
In a living polymerization, chain length simplifies to [M]0/[I]0 because all initiation leads to polymerization and there are no terminations steps. Given a radical polymerization with [M]0 = 4.5 M and [I]0 = 1.25 mM, compare chain length in the following situations:
a) a living polymerization
b) a non-living polymerization with f = 0.5; kp = kt = 0.003 s-1; kd = 0.0001 s-1.
c) a non-living polymerization with f = 0.5; kp = 0.003 s-1; kt = 0.3 s-1; kd = 0.0001 s-1.
d) a non-living polymerization with f = 0.5; kp = 0.003 s-1; kt = 0.003 s-1; kd = 0.1 s-1.
This site is written and maintained by Chris P. Schaller, Ph.D., College of Saint Benedict / Saint John's University (with contributions from other authors as noted). It is freely available for educational use.

Structure & Reactivity in Organic, Biological and Inorganic Chemistry by Chris Schaller is licensed under a Creative Commons Attribution-NonCommercial 3.0 Unported License.
Send corrections to cschaller@csbsju.edu
Support for this project was provided by the Opens Textbooks Pilot Program of the U.S. Department of Education through a collaboration with the Libre Texts project at University of California, Davis.
Navigation:
Back to Polymer Kinetics & Thermodynamics
Back to Structure & Reactivity